1.1 Conjunction, negation, disjunction
Exercise (1)
1) p – This car is powerful, q – This car is very economical: ¬p ∧ q
2) p – Bob is guilty, q – John is guilty: ¬(p∧¬q)
3) p – Voldemort is mean, q – Voldemort is cruel: p ∧ q
1.2 Conditional and biconditional
Exercise (1)
1) p – We will stay in Europe, q – We will sell the house, r – We will see you again next year: (p∧¬q)→r
3) p – The global recession will continue, q – Taxes will be reduced, r – There will be a stagnation, s – There will be bank failures: p → [¬q→(r∧s)]
5) p – Bob will go to the party, q – Alice will go to the party: p → ¬q
1.3 Truth tables. Syntax and semantics
Exercise (1)
1) It is a formula.
2) It is not a formula (parentheses are redundant).
3) It is not a formula (brackets are redundant, and it needs parentheses elsewhere).
4) It is a formula.
Exercise (2)
1) p, q, r, ¬p, ¬q, ¬p∧r, p↔¬q, (¬p∧r)∨(p↔¬q)
Exercise (3)
1) It is a conjunction.
2) It is a conditional.
3) It is a conjunction.
Exercise (4)
1) The formula is a tautology.
| p | q | q→p | p→(q→p) |
| T | T | T | T |
| T | F | T | T |
| F | T | F | T |
| F | F | T | T |
2) The formula is contingent.
| p | q | p∨q | ¬(p∨q) | p∧q | ¬(p∨q)→(p∧q) |
| T | T | T | F | T | T |
| T | F | T | F | F | T |
| F | T | T | F | F | T |
| F | F | F | T | F | F |
3) The formula is contingent.
| p | q | ¬q | p→¬q | ¬p | (p→¬q)→¬p |
| T | T | F | F | F | T |
| T | F | T | T | F | F |
| F | T | F | T | T | T |
| F | F | T | T | T | T |
4) The formula is a tautology.
| p | q | r | ¬q | ¬q∨r | p→(¬q∨r) | ¬p | ¬p∨q |
| T | T | T | F | T | T | F | T |
| T | T | F | F | F | F | F | T |
| T | F | T | T | T | T | F | F |
| T | F | F | T | T | T | F | F |
| F | T | T | F | T | T | T | T |
| F | T | F | F | F | T | T | T |
| F | F | T | T | T | T | T | T |
| F | F | F | T | T | T | T | T |
| [p→(¬q∨r)]∨(¬p∨q) |
| T |
| T |
| T |
| T |
| T |
| T |
| T |
| T |
1.4 Indirect proof
Exercise (1)
2)
| 1. (p→q)→[(r∨p)→(r∨q)] – F assumption |
| 2. p→q – Т from 1. |
| 3. (r∨p)→(r∨q) – F from 1. |
| 4. r∨p – Т from 3. |
| 5. r∨q – F from 3. |
| 6. r – F from 5. |
| 7. q – F from 5. |
| 8. p – Т from 4. and 6. |
| 9. p→q – F from 8. and 7. – contradicts 2. |
3)
| 1. [p∨(q∧¬r)]→[(p∨q)∧(r→p)] – F assumption |
| 2. p∨(q∧¬r) – T from 1. |
| 3. (p∨q)∧(r→p) – F from 1. |
| Case 1 |
| 4. p – T from 2. |
| 5. p∨q – T from 4. |
| 6. r→p – F from 3. and 5. |
| 7. p – F from 6. – contradicts 4. |
| Case 2 |
| 4. q∧¬r – T from 2. |
| 5. q – T from 4. |
| 6. ¬r – T from 4. |
| 7. r – F from 6. |
| 8. p∨q – T from 5. |
| 9. r→p – F from 3. and 8. |
| 10. r – T from 9. – contradicts 7. |
Exercise (2)
1)
| 1. (¬q→¬p)∧¬(q∨¬p) – T assumption |
| 2. ¬q→¬p – T from 1. |
| 3. ¬(q∨¬p) – T from 1. |
| 4. q∨¬p – F from 3. |
| 5. q – F from 4. |
| 6. ¬p – F from 4. |
| 7. ¬q – T from 5. |
| 8. ¬q→¬p – F from 7. and 6. – contradicts 2. |
1.5 Truth-value analysis
Exercise (1)
1) tautology
| p→(q→p) | |
| p: T | p: F |
| T→(q→T) | F→(q→F) |
| T→T | T |
| T | |
3) tautology
| (¬p∨¬q)→¬(p∧q) | |
| p: T | p: F |
| (F∨¬q)→¬(T∧q) | (T∨¬q)→¬(F∧q) |
| ¬q→¬q | T→¬F |
| T | T→T |
| T | |
4) contingent
| [(p→q)→r]↔[p→(q→r)] | |
| Case 1 p: Т | |
| [(T→q)→r]↔[T→(q→r)] | |
| [q→r]↔[q→r] | |
| T | |
| Case 2 p: F | |
| [(F→q)→r]↔[F→(q→r)] | |
| [T→r]↔T | |
| T→r | |
| r | |
| r: F | |
| F | |
Exercise (2)
2)
| (p→q)→[(r∨p)→(r∨q)] |
| Case 1 r: T |
| (p→q)→[(T∨p)→(T∨q)] |
| (p→q)→[T→T] |
| (p→q)→T |
| T |
| Case 2 r: F |
| (p→q)→[(F∨p)→(F∨q)] |
| (p→q)→[p→q] |
| T |
1.6 Logical inference and logical equivalence
Exercise (1)
6) To determine whether the inference scheme is valid, we connect the conjunction of its premises by conditional to its conclusion obtaining the formula “[(p∨¬q)∧(¬q↔¬p)]→(p→¬q)”. The scheme will be valid if this formula is a tautology. We may check whether it is a tautology by a truth table or truth-value analysis:
| [(p∨¬q)∧(¬q↔¬p)]→(p→¬q) | |
| p: T | |
| [(T∨¬q)∧(¬q↔F)]→(T→¬q) | |
| [T∧¬¬q]→¬q | |
| ¬¬q→¬q | |
| q: T | |
| T→F | |
| F | |
The formula is not a tautology, therefore the inference scheme is not valid.
Exercise (2)
2) If “The company is responsible” is symbolized by “p”, “The software is of the company” – by “q”, and “The software was installed before January” – by “r”, a) is symbolized by “p↔(q∧r)” and b) by “[q→(r∧p)]∧[¬q→(¬r∧¬p)]”. To check if b) is a logical consequence of a), we connect them into a conditional and check by a truth-value analysis (alternatively by a truth table) whether the conditional is a tautology:
| [p↔(q∧r)] → {[q→(r∧p)]∧[¬q→(¬r∧¬p)]} | |
| q: T | |
| [p↔(T∧r)] → {[T→(r∧p)]∧[F→(¬r∧¬p)]} | |
| [p↔r]→{(r∧p)∧T} | |
| (p↔r)→(r∧p) | |
| p: F | |
| (F↔r)→(r∧F) | |
| ¬r→F | |
| ¬¬r | |
| r | |
The formula is not a tautology, so b) is not a logical consequence of a).
Exercise (3)
4) To prove that the formulas are logically equivalent, we connect them into a biconditional and show by a truth-value analysis (alternatively by a truth table) that the biconditional is a tautology:
| (р↔q)↔[(p∧q)∨(¬p∧¬q)] |
| p: T |
| (T↔q)↔[(T∧q)∨(F∧¬q)] |
| q↔[q∨F] |
| q↔q |
| T |
| p: F |
| (F↔q)↔[(F∧q)∨(T∧¬q)] |
| ¬q↔[F∨¬q] |
| ¬q↔¬q |
| T |
10) Similarly:
| [р∧(q∨r)]↔[(р∧q)∨(р∧r)] | |
| p: T | |
| [T∧(q∨r)]↔[(T∧q)∨(T∧r)] | |
| (q∨r)↔(q∨r) | |
| T | |
| p: F | |
| [F∧(q∨r)]↔[(F∧q)∨(F∧r)] | |
| F↔(F∨F) | |
| F↔F | |
| T | |
Exercise (4)
4) If “John is guilty” is symbolized by “p”, “Peter is innocent” – by “q”, and “George is lying” – by “r”, a) is symbolized by “p↔(q∧r)” and b) by “[q→(r∧p)]∧[¬q→(¬r∧¬p)]”. To check if a) is logically equivalent to b), we connect them into a biconditional and check by a truth-value analysis (alternatively by a truth table) whether the biconditional is a tautology:
| [p→(q∧r)]↔[(¬r→¬p)∧(p→q)] |
| p: T |
| [T→(q∧r)]↔[(¬r→F)∧(T→q)] |
| (q∧r)↔(¬¬r∧q) |
| (q∧r)↔(r∧q) |
| T |
| p: F |
| [F→(q∧r)]↔[(¬r→T)∧(F→q)] |
| T↔(¬r∧T) |
| ¬r |
| F T |
The formula is not a tautology, so a) and b) are not logically equivalent.
1.7 Quick test of logical inference
Exercise (1)
3) The premise is true only if “p”, “r” and “s” are all true. We check whether the conclusion can then be false in that case:
| r ↔ (p→s) |
| p: T, r: T, s: T |
| T ↔ (T→T) |
| T↔T |
| T |
If the premise is true, the conclusion is also true – the inference scheme is valid.
8) The conclusion is false only if “p” and “q” are true, and “r” is false. We check whether the premise can be true in that case:
| (p∧¬q) ∨ [(r∧s)→p] |
| p: T, q: T, r: F |
| (T∧F) ∨ [(F∧s)→T] |
| F ∨ T |
| T |
The premise is true when the conclusion is false – the inference scheme is not valid.
Exercise (2)
2) p – “Our representative will run for president”, q – “Our representative will run a positive campaign”, r – “There will be a runoff”, s – “Our representative will win the election”, t – “Our representative will be reelected in four years”, u – “Our representative will support the death penalty”. The argument is symbolized by:
| p → (q→r) |
| (r∧s) → ¬t |
| u → (s∧t) |
| p → (q→¬u) |
The conclusion of the inference scheme is false only if “p”, “q” and “u” are true, so we check whether in this case the conjunction of the premises can be true:
| [p→(q→r)] ∧ [(r∧s)→¬t] ∧ [u→(s∧t)] | |
| p: T, q: T, u: T | |
| [T→(T→r)] ∧ [(r∧s)→¬t] ∧ [T→(s∧t)] | |
| r ∧ [(r∧s)→¬t] ∧ (s∧t) | |
| r: T | |
| T ∧ [(T∧s)→¬t] ∧ (s∧t) | |
| (s→¬t) ∧ (s∧t) | |
| s: T | s: F |
| (T→¬t)∧(T∧t) | (F→¬t)∧(F∧t) |
| ¬t ∧ t | T ∧ F |
| F | F |
| r: F | |
| F ∧ [(F∧s)→¬t] ∧ (s∧t) | |
| F | |
When the conclusion is false, the conjunction of the premises is also false, which means that it is not possible all of the premises to be true when the conclusion is false. So, the inference scheme and the particular inference are valid.
1.8 Natural deduction
Exercise (1)
5)
| 1. F→G |
| 2. ¬(F∧G)∧L |
| 3. (G∨H)→(I∧J) |
| 4. F∨(K∨G) |
| 5. ¬K∧L / I∨H |
| 6. F→(F∧G) 1, Abs |
| 7. ¬(F∧G) 2, S |
| 8. ¬F 6, 7, MT |
| 9. K∨G 4, 8, DS |
| 10. ¬K 5, S |
| 11. G 9, 10, DS |
| 12. G∨H 11, Add |
| 13. I∧J 3, 12, MP |
| 14. I 13, S |
| 15. I∨H 14, Add |
Exercise (2)
1)
| 1. А∨¬B |
| 2. ¬C→¬A / B→C |
| 3. ¬B∨A 1, Com |
| 4. B→A 3, Imp |
| 5. A→C 2, Trans |
| 6. B→C 4, 5, HS |
Exercise (3)
5)
| 1. (L∧M)→N |
| 2. (L∧¬M)→¬N / L→(M↔N) |
| 3. L→(M→N) 1, Exp |
| 4. L→(¬M→¬N) 2, Exp |
| 5. L→(N→M) 4, Trans |
| 6. ¬L∨(M→N) 3, Imp |
| 7. ¬L∨(N→M) 5, Imp |
| 8. [¬L∨(M→N)]∧[¬L∨(N→M)] 6, 7, Conj |
| 9. ¬L∨[(M→N)∧(N→M)] 8, Distr |
| 10. ¬L∨(M↔N) 9, Equiv |
| 11. L→(M↔N) 10, Imp |
Exercise (4)
5)
| 1. (L∧M)→N |
| 2. (L∧¬M)→¬N / L→(M↔N) |
| 3. L→(M→N) 1, Exp |
| 4. L→(¬M→¬N) 2, Exp |
| 5. L→(N→M) 4, Trans |
| 6. L assumption |
| 7. M→N 3, 6, MP |
| 8. N→M 5, 6, MP |
| 9. (M→N)∧(N→M) 7, 8, Conj |
| 10. M↔N 9, Equiv |
| 11. L→(M↔N) 6–10, conditional proof |
Exercise (5)
3) The simple sentences in the argument are the following: I – “The doctor will inject the antibodies”, A – “The patient will have an allergic reaction”, K – “The patient’s kidney will stop functioning”, B – “The bacteria will spread to the bloodstream”, S – “The patient will survive until the morning”. The argument is symbolized as follows
| (I→A)∧(A→K) |
| ¬I→B |
| B→K |
| K→¬S |
| I∨¬I |
| ¬S |
Here are two proofs of its validity – with and without proofs by assumption:
| 1. (I→A)∧(A→K) |
| 2. ¬I→B |
| 3. B→K |
| 4. K→¬S / ¬S |
| 5. B→¬S 3, 4, HS |
| 6. I→A 1, S |
| 7. A→K 1, S (and Com) |
| 8. I→K 6, 7, HS |
| 9. ¬I→K 2, 3, HS |
| 10. ¬K→¬I 8, Trans |
| 11. ¬K→K 10, 9, HS |
| 12. ¬¬K∨K 11, Imp |
| 13. K∨K 12, DN |
| 14. K 13, Taut |
| 15. ¬S 4, 14, MP |
| 1. (I→A)∧(A→K) |
| 2. ¬I→B |
| 3. B→K |
| 4. K→¬S / ¬S |
| 5. ¬¬S assumption |
| 6. ¬K 4, 5, MT |
| 7. ¬B 3, 6, MT |
| 8. ¬¬I 2, 7, MT |
| 9. I 8, DN |
| 10. I→A 1, S |
| 11. A 9, 10, MP |
| 12. A→K 1, S (and Com) |
| 13. K 11, 12, MP – contradicts 6 |
| 14. ¬S 5–13, reductio ad absurdum |
1.9 Logical transformations
Exercise (1)
1) The formula is in both disjunctive normal form and conjunctive normal form.
10) The formula is neither in disjunctive normal form nor in conjunctive normal form.
Exercise (2)
11)
| [(r→¬s)→r] ∧ {(r∧s) ∨ [¬r→¬(p→q)]} |
| [¬(r→¬s)∨r] ∧ {(r∧s) ∨ ¬¬r ∨ ¬(p→q)} |
| [(r∧¬¬s)∨r] ∧ {(r∧s) ∨ r ∨ (p∧¬q)} |
| r ∧ {r ∨ (p∧¬q)]} |
| r |
Exercise (3)
4) Through the transformations below, the two formulas are reduced to the same formula; so, they are logically equivalent.
| first formula: |
| p → (¬q∧r) |
| ¬p ∨ (¬q∧r) |
| (¬p∨¬q) ∧ (¬p∨r) |
| second formula: |
| (p→¬q) ∧ (p→r) |
| (¬p∨¬q) ∧ (¬p∨r) |
Exercise (5)
3) Through the transformations below, the formula is reduced to an expression of the form α→α; so, it is a tautology.
| [p∨(q∧¬r)] → [(p∨q)∧(r→p)] |
| [p∨(q∧¬r)] → [(p∨q)∧(¬r∨p)] |
| [p∨(q∧¬r)] → [(p∨q)∧(p∨¬r)] |
| [p∨(q∧¬r)] → [(p∨(q∧¬r)] |
2. Traditional logic
2.1 Categorical sentences
Exercise (1)
5) The sentence is in standard form. It is a universal affirmative and has “active opponent of the corporative tax raise” as a subject and “member of the Chamber of Commerce” as a predicate. Its symbolic representation is “SaP”.
17) Rephrased in standard form, the sentence becomes “All who are capable of loving have known misfortune”. So, it is universal affirmative with a subject “(a person) who is capable of loving” and a predicate “(a person) who has known misfortune”. Its symbolic representation is “SaP”.
2.2 Square of opposition
Exercise (1)
2) When an A-sentence is false, the corresponding E and I-sentences are undetermined and the O-sentence is true.
2.3 Immediate inferences
Exercise (1)
7) By subalternation we can infer “Some optimists are not persons who know life”; by inversion – “No persons who know life are optimists”; by obversion – “All optimists are persons who do not know life”; by contraposition – “Some persons who do not know life are optimists”.
2.4 Syllogisms
Exercise (1)
1) The conclusion is “Some space bodies move in elliptical orbits”; it subject “space body” is the minor term and its predicate “something that moves in elliptical orbit” is the major term. The middle term is “planet”. The major premise contains the major term; hence, it is “All planets move in elliptical orbits”. The other premise, “All planets are space bodies”, is the minor premise. The syllogism’s standard form is
| All planets move in elliptical orbits. |
| All planets are space bodies. |
| Some space bodies move in elliptical orbits. |
Its symbolic representation is
| MaP |
| MaS |
| SiP |
Its type is AAI-3.
Exercise (2)
1)
| 1. PeM |
| 2. SiM / SoP |
| 3. MeP 1, conversion |
| 4. SоP 3, 2, EIO-1 (Ferio) |
2.5 Syllogistic rules
Exercise (1)
1) In a more detailed form IAI-2 is symbolized as follows:
| PiM |
| SaM |
| SiP |
The only broken rule is that the middle term is not distributed in any of the premises.
Exercise (2)
1) The argument is symbolized by
| MoP |
| SaM |
| SoP |
where S corresponds to “a good physicist”, M to “a good mathematician”, P to “has a high spatial intelligence”. The syllogism is invalid as it violates the rule that the middle term has to be distributed at least in one of the premises.
2.6 Venn diagrams
Exercise (1)
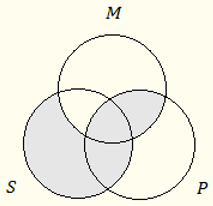
1) Represented in a more extended symbolic form, EAE-1 is the following inference scheme:
| MeP |
| SaM |
| SeP |
The diagram below shows that it is logically valid.
3. Predicate logic
3.1 General and singular terms
Exercise (1)
5) general term
Exercise (2)
5) F – …is trustworthy, a – what he said now, b – what he said earlier: Fa ∧ ¬Fb
3.2 Variables and quantifiers
Exercise (1)
4) The scope of “∃x” is “Fxy ∧ ∀yGyx”; the scope of “∀y” is “Gyx”. The two occurrences of “x” are bound; the first occurrence of “y” is free and the second is bound. The formula symbolizes an open sentence.
Exercise (2)
14) ∃x(Hx ∧ Gx ∧ Fax)
3.3 The advantages of predicate logic
Exercise (1)
12) ∀x[(Fx ∧¬Hxa) → Gax]
20) ∀x∃y(Fxy ∧ Fya)
Exercise (2)
3) ∀x[Hx → ∃y(Hy ∧ Fxy ∧ Fya)]
3.5 Proof procedure
Exercise (1)
6) After we move the negation in the first expression (“¬∃x∀y∀z”) on the other side of the quantifiers and switch them, we get “∀x∃y∃z¬”. This expression differs from the second one (“∀x∃y∀z¬”) only in the last quantifier. Therefore, if we change “∀z” to “∃z” in the first expression, the two expressions will become equivalent.
Exercise (2)
6) It is incorrect. The premise (“¬∀x(Fxa ↔ Gax)”) has the form of a negation – it must be a universal or existential sentence.
Exercise (3)
5) Both instantiations are incorrect: the existential one – because the instantiated constant “a” is not new, the universal one – because the formula in 1. is not a universal sentence (it is a negation).
Exercise (4)
3) Symbolized in the language of predicate logic, OAO-3 is the following inference scheme:
| ∃x(Mx ∧ ¬Px) |
| ∀x(Mx → Sx) |
| ∃x(Sx ∧ ¬Px) |
| 1. ∃x(Mx ∧ ¬Px) |
| 2. ∀x(Mx → Sx) / ∃x(Sx ∧ ¬Px) |
| 3. ¬∃x(Sx ∧ ¬Px) assumption |
| 4. ∀x¬(Sx ∧ ¬Px) 3, RbQ |
| 5. Ma ∧ ¬Pa 1, EI |
| 6. Ma → Sa 2, UI |
| 7. ¬(Sa ∧ ¬Pa) 4, UI |
| 8. Ma 5, S |
| 9. Sa 8, 6, MP |
| 10. ¬Pa 5, S |
| 11. Sa ∧ ¬Pa 9, 10, Conj – contradicts 7 |
| 12. ∃x(Sx ∧ ¬Px) 3–11, reductio ad absurdum |
Exercise (5)
5)
| 1. ∃x(Fx∧Gx) ∨ ∃x(Fx∧¬Gx) / ∃xFx |
| 2. ¬∃xFx assumption |
| 3. ∀x¬Fx 2, RbQ |
| 4. ∃x[(Fx∧Gx) ∨ (Fx∧¬Gx)] 1, distribution of the existential quantifier over disjunction |
| 5. (Fа∧Gа) ∨ (Fа∧¬Gа) 4, EI |
| 6. Fа ∧ (Gа∨¬Gа) 5, Distr |
| 7. Fа 6, S |
| 8. ¬Fа 3, UI – contradicts 7 |
| 9. ∃xFx 2–8, reductio ad absurdum |
Exercise (6)
9)
| 1. ∀x[Fx → (Gx ∧ Hx) |
| 2. ∃x(Hx ∧ ¬Gx) / ∃x(¬Fx ∧ Hx) |
| 3. ¬∃x(¬Fx ∧ Hx) assumption |
| 4. ∀x¬(¬Fx ∧ Hx) 3, RbQ |
| 5. Hа ∧ ¬Gа 2, EI |
| 6. Fa → (Ga ∧ Ha) 1, UI |
| 7. ¬(¬Fa ∧ Ha) 4, UI |
| 8. Fa ∨ ¬Ha 7, De M and DN |
| 9. Ha 5, S |
| 10. Fa 8, 9, DS |
| 11. Ga ∧ Ha 10, 6, MP |
| 12. Ga 11, S |
| 13. ¬Gа 5, S – contradicts 12 |
| 14. ∃x(¬Fx ∧ Hx) 3–13, reductio ad absurdum |
Exercise (7)
2) We assume the negation of “∃x(∀yFy→Fx)” and come to a contradiction:
| 1. ¬∃x(∀yFy → Fx) assumption |
| 2. ∀x¬(∀yFy → Fx) 1, RbQ |
| 3. ¬(∀yFy → Fа) 2, UI |
| 4. ∀yFy ∧ ¬Fа 3, Imp |
| 5. ∀yFy 4, S |
| 6. ¬Fа 4, S |
| 7. Fа 5, UI – contradicts 6 |
| 8. ∃x(∀yFy → Fx) 1–7, reductio ad absurdum |
Exercise (9)
5) The relation is irreflexive (no one is their own teacher); it is neither symmetric nor asymmetric (if a is a teacher of b, then b may be a’s teacher in something else or may not be a’s teacher at all); it is neither transitive nor intransitive (if a is a teacher of b and b is a teacher of c, a may or may not be c’s teacher).
3.6 Identity
Exercise (2)
8) ¬∃x∃y[Fxy ∧ ∀z(z≠y → ¬Fyz)]
Exercise (5)
4) ∃x{Fx ∧ Gax ∧ ∀y[(Fy ∧ Gay) → x=y] ∧ Hxc}
3.7 Logical transformations in predicate logic
Exercise (1)
7) We convert the first formula to the second with the following series of equivalences:
| ∀xFxy ↔ ¬∃zGz |
| (∀xFxy → ¬∃zGz) ∧ (¬∃zGz → ∀xFxy) |
| (∀xFxy → ∀z¬Gz) ∧ (∀z¬Gz → ∀xFxy) |
| ∃x(Fxy → ∀z¬Gz) ∧ ∀x(∀z¬Gz → Fxy) |
| ∃x(Fxy → ∀z¬Gz) ∧ ∀x∃z(¬Gz → Fxy) |
Exercise (2)
4)
| ∃xFx → [∃xGx ↔ ∃xHx] |
| ∃xFx → [(∃xGx → ∃xHx) ∧ (∃xHx → ∃xGx)] |
| ∃xFx → [(∃yGy → ∃zHz) ∧ (∃wHw → ∃uGu)] |
| ∀x{Fx → [(∃yGy → ∃zHz) ∧ (∃wHw → ∃uGu)]} |
| ∀x{Fx → [∀y(Gy → ∃zHz) ∧ ∀w(Hw → ∃uGu)]} |
| ∀x{Fx → [∀y∃z(Gy → Hz) ∧ ∀w∃u(Hw → Gu)]} |
| ∀x{Fx → ∀y∃z[(Gy → Hz) ∧ ∀w∃u(Hw → Gu)]} |
| ∀x{Fx → ∀y∃z∀w∃u[(Gy → Hz) ∧ (Hw → Gu)]} |
| ∀x∀y∃z∀w∃u{Fx → [(Gy → Hz) ∧ (Hw → Gu)]} |
4. Non-classical logics
4.1 Modal logic
Exercise (1)
11) ◊f p → □p◊f p
Exercise (2)
6) They are not equivalent but they will become so if ¬◊□□α (the first scheme) is changed to ¬◊□◊α.
Exercise (3)
10)
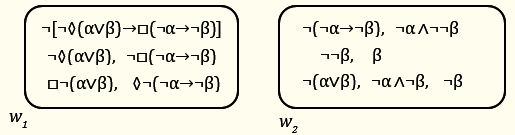
Exercise (4)
7)

Exercise (5)
7)
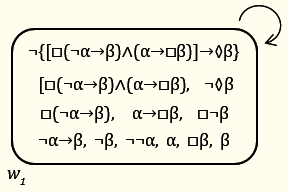
Exercise (6)
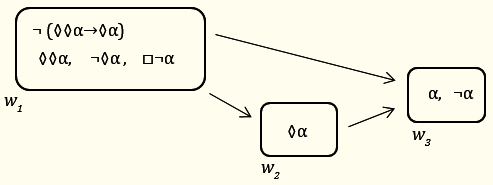
1)
Exercise (8)
3)

4.2 Three-valued logic
Exercise (1)
3) Where the values are two, the first is for Kleene’s logic and the second for Bochvar’s.
| p | q | ¬p | ¬q | q∧¬q | ¬p∨(q∧¬q) |
| T | T | F | F | F | F |
| T | # | F | # | # | # |
| T | F | F | T | F | F |
| # | T | # | F | F | # |
| # | # | # | # | # | # |
| # | F | # | T | F | # |
| F | T | T | F | F | T |
| F | # | T | # | # | T # |
| F | F | T | T | F | T |