Да бъдеш логичен означава, когато се аргументираш или разсъждаваш, да използваш само валидни аргументи. Логиката е научното изследване на валидните аргументи.
Всеки аргумент представлява извод, който има предпоставки и заключение. Както предпоставките, така и заключението са изречения. Ето два примера:
| Иван не е болен от грип, защото, ако беше, щеше да има температура, а той няма. |
| Ако Иван е болен от грип, той ще има температура, и тъй като има температура, значи е болен от грип. |
И двата извода имат по две предпоставки. Когато анализираме някакъв извод, ще записваме предпоставките му една под друга, като под тях, отделено с черта, ще записваме заключението:
| Ако Иван е болен от грип, той има температура. |
| Иван няма температура. |
| Иван не е болен от грип. |
| Ако Иван е болен от грип, той има температура. |
| Иван има температура. |
| Иван е болен от грип. |
Един извод е валиден, когато не е възможно предпоставките да са истинни, а заключението да е неистинно; и е невалиден, когато това е възможно. От горните два извода първият е валиден, защото, ако двете му предпоставки са истинни, няма как заключението да е неистинно. Напротив, вторият е невалиден, защото е възможно Иван да има температура и да не е болен от грип (а от нещо друго) – тогава предпоставките биха се оказали истинни, а заключението не. Първият извод е пример за логично, а вторият за нелогично разсъждение. В първия случай е налице логическо следване, а във втория не.
Един извод е логически валиден, когато е (логически) невъзможно предпоставките му да са истинни, а заключението да е неистинно. Тогава казваме, че заключението следва логически от предпоставките. Логическото следване е от основен интерес за логиката, затова важен логически въпрос е как по принцип (чрез общ метод) да може да бъде определяно дали от дадени предпоставки логически следва дадено заключение. Друг важен въпрос е как по принцип (чрез общ метод), ако дадено заключение (обективно) следва от дадени предпоставки, това да може да бъде ясно показано (доказано). Без да са един и същ въпрос, двата въпроса са свързани и съвсем не са тривиални. Съвременната логика показва, че първият е принципно нерешим в своята всеобщност – т.е. няма и не може да има универсален алгоритъм, обща рецепта, чрез която да разбираме дали от дадени предпоставки следва дадено заключение. Вторият обаче е решим – има общи доказателствени процедури, чрез които, ако едно заключение следва (обективно) от някакви предпоставки, това може да бъде доказано.
Предпоставките и заключението на всеки извод са изречения, но не какви да е изречения, а такива, които могат да бъдат (и са) истинни или неистинни. Ще наричаме такива изречения „твърдения“. От долните изречения само последното е твърдение
| Утре вторник ли е? |
| Кажи какво мислиш без да се притесняваш. |
| Ех, да бях 20 години по-млад! |
| Всички гъби са растения. |
Въпросите, заповедите, молбите, възклицанията и т.н. са изречения, но не са твърдения, защото не са истинни или неистинни.
Важно е да се прави разлика между логическата валидност или невалидност на един извод и истинността или неистинността на твърденията, които го съставят. Това дали някакво заключение следва логически от някакви предпоставки няма нищо общо с това дали предпоставките и заключението му са истинни, или не. Да разгледаме следните два извода:
| Всички същества с крила са богове. |
| Всички хора имат крила. |
| Всички хора са богове. |
| Всички хищници са животни. |
| Всички тигри са животни. |
| Всички тигри са хищници. |
В първия извод и трите твърдения са неистинни, а във втория и трите са истинни, но въпреки това първият е логически валиден, а вторият не е. Всеки човек, който би направил първия извод, би бил по-логичен от всеки, който би направил втория, въпреки че светът (като светоглед), в който първият човек би живял, би бил много по-отдалечен от действителността от този на втория, по-нелогичен човек. Причината за логическата валидност на първия извод е, че, ако предпоставките му бяха истинни, заключението му щеше (по необходимост) също да бъде истинно – т.е. невъзможно е предпоставките да са истинни и в същото време заключението да е неистинно, което, както посочихме по-горе, е критерият за логическа валидност на един извод. Напротив, въпреки че всички твърдения във втория извод са истинни, би било възможно двете предпоставки да са истинни, а заключението да е неистинно, защото не е (логически) невъзможно (макар и да не е факт) тигрите и хищниците да са животни, без тигрите да са хищници. Долната диаграма показва защо е така.
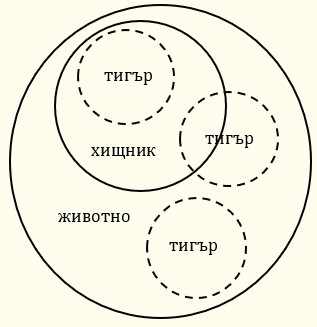
Кръговете в диаграмата отговарят на съответните множества от неща. Например това, че кръгът на хищниците е включен напълно в кръга на животните, съответства на положението на нещата множеството на хищниците да е подмножество на множеството на животните, т.е. на това, всички хищници да са животни (първата предпоставка). Това, че в диаграмата както кръгът на хищниците, така и кръгът на тигрите е включен в кръга на животните, отговаря на приемането, че и двете предпоставки („Всички хищници са животни“ и „Всички тигри са животни“) са истинни. При това приемане кръгът на тигрите (ограден с пунктирана линия) би могъл да има три различни положения спрямо кръга на хищниците – може напълно да се включва в него (каквото е фактическото положение на нещата), само отчасти да се включва, или напълно да се изключва. Вторите два случая биха направили заключението („Всички тигри са хищници“) неистинно, като в същото време истинността на двете предпоставки би се запазила. Това показва, че е (логически) възможно предпоставките да са истинни, а заключението да е неистинно, което значи, че изводът е невалиден – че не гарантира истинност на заключението при истинност на предпоставките.
Напротив, долната диаграма показва, че ако предпоставките на първия извод бяха истинни, няма как заключението да е неистинно.

Ако предпоставките („Всички същества с крила са богове“ и „Всички хора имат крила“) бяха истинни, кръгът на крилатите същества щеше да се включва напълно в кръга на боговете, а този на хората – в кръга на крилатите същества (както е на диаграмата). Но тогава няма как кръгът на хората да не се включва в този на боговете – т.е. няма как заключението да e неистинно, ако предпоставките бяха истинни. Това ни показва, че изводът е логически валиден, въпреки че изреченията, от които е съставен, са фактически неистинни. Логиката е отвъд фактическото положение на нещата – тя взима предвид всеки възможен свят.
Определяща за логическата валидност или невалидност на един извод е неговата структура, а не думите, които го изграждат, т.е. важна е формата на извода, а не съдържанието му. Например, както и да променяме съдържанието на изреченията в горните два извода, като променяме думите в тях, стига само да запазим структурата им като цяло (т.е. да запазим логическата им форма), първият извод ще продължи да бъде логически валиден, а вторият – логически невалиден. Например долните два извода са получени от горните, като са сменени думи и изрази в тях, в резултат на което предметът на изреченията е напълно променен; цялостната форма на изводите обаче е същата:
| Всеки, който си е забравял чадъра у нас, е бил мъж. |
| Всички мои приятели, родени през март, са си забравяли чадъра у нас. |
| Всички мои приятели, родени през март, са мъже. |
| Всяка катерица е бозайник. |
| Всеки слон е бозайник. |
| Всеки слон е катерица. |
Първият извод е получен от първия по-горе, като изразът „същество с крила“ е заменен с „(човек), който си е забравял чадъра у нас“, думата „бог“ е заменена с „мъж“ и думата „човек“ с израза „мой приятел, роден през март“, а второто е получено от второто по-горе, като думата „хищник“ е заменена с „катерица“, „животно“ с „бозайник“ и „тигър“ със „слон“. В резултат на замяната всяко от трите неистинни изречения в първия извод се е превърнало в изречение, което би могло да е както истинно, така и неистинно (зависи кой го казва), а във втория извод предпоставките продължават да бъдат истинни, но заключението е станало неистинно. Всички тези замени не променят валидността (невалидността) на изводите – първият от втората двойка продължава да е валиден, а вторият – не, и причината е същата, показана чрез диаграмите по-горе.
Тъй като за логическата валидност или невалидност на един извод е определяща неговата форма, а не съдържанието му, в логиката се използват символи, които заместват думи или изрази в изреченията, така че да изпъкне логическата форма. Така например, ако заменим част от думите и изразите в четирите разгледани по-горе изводи със символите „S“, „M“ и „P“, ще направим явна логическата им форма, която на двата валидни извода (първите в двете двойки) е
| Всички M са P. |
| Всички S са М. |
| Всички S са P. |
а на двете невалидни:
| Всички P са М. |
| Всички S са М. |
| Всички S са P. |
Съответно това, че всеки извод, който има първата форма, е логически валиден и всеки, който има втората, е логически невалиден, се вижда от следните две диаграми.


Нека повторим: това, дали един извод е логически валиден, или не, се определя от логическата му форма, а не от съдържанието на твърденията, които участват в него, нито от това, дали тези твърдения са истинни, или не. Затова (въпреки че между двете има връзка) да бъдем логични и да говорим истината са две различни неща. Човек може да прави само логически валидни изводи, но ако тръгва от неистинни предпоставки, е много вероятно да стигне до неистинни заключения; и обратно – въпреки че прави невалидни изводи, някой би могъл да тръгне от истинни предпоставки и (по случайност) да стигне до истинни заключения. Това което логическата валидност гарантира е, че ако предпоставките са истинни, и заключенията ще са такива. Така че идеалният случай е да тръгваме от истинни предпоставки и да правим само логически валидни изводи – тогава ще имаме най-силната възможна гаранция (логическата), че твърденията, до които стигаме, ще бъдат истинни.
Ако това, което прави изводите логически валидни или невалидни, е логическата им форма, то в какво по-определено се състои тя? Логическата форма на един извод зависи от логическата форма на съставящите го твърдения (предпоставките и заключението), а тяхната форма зависи от думи или изрази, които бихме могли да наречем логически. Такива са например думите „всички“ („всеки“) и „са“ („е“). По-горе направихме явна логическата форма на изводи, които ги съдържат, като заменихме останалите, нелогически думи и изрази в тях със символи („S“, „M“ и „P“). Така получихме две схеми за извод:
| Всички M са P. | Всички P са М. | |
| Всички S са М. | Всички S са М. | |
| Всички S са P. | Всички S са P. |
Независимо с какви думи или изрази заместваме символите „S“, „M“ и „P“ (един и същ символ – с една и съща дума или израз), от първата схема винаги ще се получава логически валиден извод, а от втората – логически невалиден.
По същия начин стоят нещата с примерите за валиден и невалиден извод, които дадохме в началото:
| Ако Иван е болен от грип, той има температура. |
| Иван няма температура. |
| Иван не е болен от грип. |
| Ако Иван е болен от грип, той има температура. |
| Иван има температура. |
| Иван е болен от грип. |
Логическата форма на тези два извода се определя от логическите изрази „ако …, то …“ и „не“1. Като заместим останалите, съдържателни изрази в тях, които в случая са цели изречения, със символи, получаваме следните две схеми за извод:
| Ако A, то B. | Ако A, то B. | |||
| Не-B. | B | |||
| Не-А. | A |
Всеки извод, който има формата на първата схема (т.е., който се получава от нея чрез заместване на „A“ и „B“ с някакви твърдения), ще е логически валиден, и всеки, който има формата на втората, ще е логически невалиден.
Ето примери за логически думи и изрази:
„всеки“ „някой“ „никой“ „е“ „съществува“ „и“ „или“ „ако …, то …“ „само ако“ „нито …, нито …“ „освен ако“ „идентично“ „друго“ „необходимо“ „възможно“
Логическите, за разлика от нелогическите (съдържателните), думи или изрази се срещат във всички области. Това отговаря на факта, че (независимо от областта), когато се говори рационално, се дават аргументи (правят се изводи); валидността на аргументите (изводите) зависи от логическата им форма, а тя пък зависи от тези думи или изрази – не от съдържанието на изреченията. Ако човек е логичен, той ще е такъв независимо дали ще се занимава с политика, философия, биология и т.н. (по същия начин и ако е нелогичен).
Аристотел (4 в. пр.н.е.) поставя началото на логиката като наука. В центъра на неговите логически занимания са така наречените „силогизми“. Това са определен вид изводи, в които участват логическите думи „всички“, „някои“, „нито един“ и др. Повечето примери по-горе бяха силогизми. Силогизъм е например логически валидният извод
| Всички същества с крила са богове. |
| Всички хора имат крила. |
| Всички хора са богове. |
Логическите съчинения на Аристотел са наречени от неговите последователи (перипатетиците) „Органон“ („инструмент“ на гръцки). Органонът включва книгите Категории, Топика, За интерпретацията, Първа аналитика и Втора аналитика.
Аристотел демонстрира две ключови характеристики на логиката:
| 1) | абстрахиране от съдържанието и интерес към формата |
| 2) | използване на символи с цел експлициране на формата |
Той формулира два принципа, които поставя в основата на всяко теоретично занимание: законът за непротиворечието и законът за изключеното трето. Първият гласи, че едно твърдение и неговото отрицание не могат да са едновременно истинни, а вторият – че поне едното от тях трябва да е истинно. Например ние не знаем дали има, или няма извънземен живот, но законът за непротиворечието ни гарантира, че не може и двете да са факт (не може както твърдението „Има извънземен живот“, така и твърдението „Няма извънземен живот“ да са истинни). От друга страна законът за изключеното трето гарантира, че поне едното е факт (поне едното от твърденията „Има извънземен живот“ и „Няма извънземен живот“ е истинно).
Логическата теория на Аристотел има огромно влияние върху западната мисъл. По същество тя изчерпва почти всичко, което западният свят има като логика от края на Античността чак до края на 19 в., когато възниква съвременната логика.
Мегаро-стоическата логика води началото си от Евклид от Мегара (5 – 4 в. пр.н.е.), ученик на Сократ и съвременник на Платон. Учениците му били наричани „мегарци“, а по-късно „диалектици“. Под „диалектика“ древните гърци разбирали размяна на аргументи и контрааргументи между защитници на някаква теза и нейната антитеза, в резултат на което би могло да се стигне до отхвърляне на една от двете позиции или до някаква форма на комбинация (синтез) между тях. Значими фигури сред мегарците били Диодор Крон (4 – 3 в. пр.н.е.) и неговият ученик Филон (4 – 3 в. пр.н.е.).
По-късно (3 в. пр.н.е.) логическите възгледи на мегарците били възприети и систематизирани от стоиците, от където идва и названието „мегаро-стоическа логика“. Най-значим логик между стоиците бил Хризип (3 в. пр.н.е.), който написал над 300 логически съчинения, от които обаче никое не оцеляло.
Едно от нещата, с които представителите на мегаро-стоическата логика се занимавали, били въпросите за необходимостта и възможността. Например Диодор настоявал, че „невъзможното не следва от възможното“, докато Хризип отричал това. (В наше време с необходимостта и възможността се занимава модалната логика.)
Освен това ги интересувало кога едно условно твърдение (изречение от вида „Ако А, то В“) е истинно. Филон смятал, че за да е истинно, е достатъчно нещата да не стоят така, че A да е истинно, а B да е неистинно, докато Диодор твърдял, че за да е истинно, трябва да не е възможно, А да е истинно, а B да е неистинно. Първият възглед отговаря на съвременното разбиране за материална импликация, а вторият – за строга импликация. Изобщо забележителна разлика между мегаро-стоическата логика и логиката на Аристотел е, че представителите на първата се интересували от логическите връзки, чрез които твърденията се свързват в по-сложни твърдения, като израза „ако …, то …“, докато Аристотеловата логика напълно ги игнорира. В наше време с тези връзки се занимава пропозиционалната логика.
Друго, което интересувало представителите на мегаро-стоическата логика, било понятието за значение. Стоиците например смятали, че това, което едно изречение изразява (не нещата, за които говори, а самото му значение), е нещо реално. В наше време терминът за такова реално, отговарящо на значението на едно твърдение нещо, е „пропозиция“ (друг е въпросът, че много философи не вярват, че такова нещо съществува).
В продължение на векове мегаро-стоическата (а не Аристотеловата) логика била доминиращото логическо учение в античния свят. След края на Римската империя (5 в.) не оцелели никакви оригинални произведения на мегаро-стоическата логика. Това е причината за изчезването на тази логическа традиция. Аристотеловата логика имала по-голям късмет.
През така наречените „тъмни векове“ (5 – 10 в.) една от малкото връзки с логиката на древните гърци бил християнският философ Боеций (5 – 6 в.), който бил запознат с част от логическите съчинения на Аристотел. До 12 в. единствените достъпни Аристотелови съчинения в западния свят били Категории и За интерпретацията. В началото на 13 в. западът открил и останалите съчиненията от Органона (Първа и Втора аналитика и Топика), в резултат на което възникнала така наречената схоластическа логика – рафинирана форма на Аристотеловата логика, доразвиваща я в детайлите.
В широк смисъл, под термина традиционна логика се разбира Аристотеловата логика, противопоставена на съвременната логика. В по-тесен смисъл под термина се разбира характерният за Новото време, психологизиран вариант на Аристотеловата логика, началото на който слага един учебник по логика, написан в края на 17 в. – Логика, или изкуството на мисленето (1662) от Антуан Арно и Пиер Никол, който става по-известен като Логиката на Пор Роял. Пор Роял е манастир във Франция, център на теологическото движение на янсенизма. Двамата автори на учебника са видни негови представители, повлияни от философските възгледи на Декарт. Част от учебника вероятно е написана от Блез Паскал. Учебникът придобива огромна популярност и става стандартният учебник по логика във Франция и Англия през 17 и 18 в. Като логическо съдържание традиционната логика (в този по-тесен смисъл, свързан с въпросния учебник) следва Аристотеловата, но я психологизира. Докато Аристотел и следващата го схоластическа традиция разглеждат логическата форма като форма на аргументите и твърденията – т.е. като форма на неща от езика, традиционната логика отнася логическата форма към мислите или представите и начините им на свързване в съзнанието. За традиционната логика (в тесния смисъл) логическата форма е форма на феномени от мисленето или съзнанието вместо от езика. Вместо за думата „човек“ традиционната логика би говорила за понятието „човек“; вместо за твърдението „Човекът е смъртен“ – за съждението „Човекът е смъртен“; вместо за някакви, изразявани чрез езика, изводи – за умозаключения като процеси на съзнанието и т.н. В своята крайна форма такъв подход към логиката я разглежда като подчинена на психологията и се нарича „психологизъм в логиката“ (термин с негативно значение).
В края на 19 и началото на 20 в., когато възниква съвременната логика, това психологизиране на логиката спира. Съвременното разбиране за логика, дори в по-голяма степен от Аристотел, я свързва с езика – изводите са последователности от твърдения (езикови неща) и тяхната форма (това, което ги прави логически валидни, или не) зависи от определени логически думи или изрази.
В началото на 20 в. възниква предикатната логика, наричана още логика от първи ред, която се утвърждава като класическата съвременна логика. Нейните възможности за логически анализ са много по-големи от тези на традиционната (Аристотелова) логика. Част от нея, пропозиционалната логика, се занимава с изводите, чиято логическа валидност зависи от така наречените логически съюзи – логически думи или изрази (като „и“, „или“, „ако …, то …“ и др.), които свързват твърдения в по-сложни твърдения. В обхвата на пропозиционалната логика са например споменатите по-горе схеми за извод
| Ако A, то B. | Ако A, то B. | |||
| не-B | B | |||
| не-А | A |
Извън обхвата на пропозиционалната логика, но в този на съдържащата я предикатна логика, са изводите, чиято логическа валидност зависи от логически думи като „някои“, „всички“, „никой“, „съществува“ и др. Аристотеловите силогизми са такива, но те са само част (макар и важна) от всички такива изводи. Съществуват много други видове изводи, които не могат да бъдат анализирани адекватно със средствата на традиционната логика. Логическият инструментариум на предикатната логика е много по-мощен и ѝ позволява да анализира адекватно всеки такъв извод.
Предикатната и пропозиционалната логика (втората е част от първата) са това, което можем да наречем класическа съвременна логика. Освен това има техни разширения или алтернативи, които понякога се наричат некласически логики. Преди всичко тук спада групата на модалните логики. Това са разширения на класическата логика, които се получават, като към логическите символи на последната се добавят така наречените модални оператори. Модалните оператори са символният еквивалент на думи като „необходимо“, „възможно“, „позволено“, „задължително“ и др. Модалните логики се различават помежду си по това, кои са въпросните думи, на които добавените модални оператори отговарят. В алетичната модална логика това са „необходимо“ и „възможно“; в деонтичната модална логика това са „задължително“ и „позволено“; в темпоралната модална логика това са изрази, свързани с миналото и бъдещето, като „винаги е било“, „някога е било“, „винаги ще бъде“, „някога ще бъде“; в епистемичната модална логика – думи като „знае“, „вярва“ и др.
Модалните логики са опити за разширение на класическата логика, защото приемат нейните принципи, като се стремят да увеличат обхвата ѝ. Освен тях има и алтернативи на класическата логика, които отхвърлят нейни основни принципи, заменяйки ги с други. Такава е например тризначната логика, в която се отхвърля принципът на бивалентността. Този принцип гласи, че всяко твърдение е истинно или неистинно. В тризначната логика се приема, че някои твърдения не са нито истинни, нито неистинни, а имат някаква трета истинностна стойност – например неопределено или безсмислено.